

在上一文章中,我们为 APMM 机制的出现做了大量的铺垫,今天我们可以欢迎我们的主角登场。
还记得最后我们所讨论的一个真正好的预测市场协议应该满足哪些条件么?
简单可以归纳为三个点:可以适用于低流动性的长尾预测市场,预测市场的发布应由用户灵活设置,以及任何人都可以成为预测市场的流动性提供者。
APMM 的出现可以完美满足这些需求。
06 APMM 的交易设计
6.1 数学约束
在上一章中,我们提出了预测市场协议设计的三个核心数学约束:
价格总和约束:所有选项的市场价格之和应为 1
清算一致性约束:事件落地时,胜出选项的清算价格应为 1
初始定价灵活性:协议应允许灵活设置初始价格状态
这三项约束共同构成了一个预测市场机制是否“完备”的核心判据。我们将在本节中展开分析,说明为何这三点重要,并讨论 APMM 如何满足全部约束。
约束一 & 约束二的冲突与可解性
我们先从业界已有机制入手:
在 CLOB + CTF 模型下,第 2 条(清算价为 1)可以通过条件代币框架(CTF)严格实现;但由于不同选项被拆分为多个二元市场,其 YES 价格往往无法归一,无法保证价格总和为 1。
而 LMSR(Logarithmic Market Scoring Rule)机制在理论上可以完美保证所有价格之和为 1,但由于每个选项的代币供应量不同,胜出选项的清算价格不一定为 1,从而违背了第 2 条约束。
这引出了一个关键问题:
是否存在一种机制,能够在数学上同时满足“价格归一”与“清算归一”?
答案是肯定的。我们可以从第 2 条入手,反推满足条件所需的系统结构。
从清算一致性推导:资产 - 储备对等原则
若希望胜出选项的清算价格严格等于 1,那么系统中必须具备足够的 USD 储备,用于以 1:1 的比例赎回对应代币。
因此,一个关键结论是:
是否存在一种机制,能够在数学上同时满足“价格归一”与“清算归一”?
这正是 CTF 机制的基本原理:
用户投入 1 USD,系统铸造所有选项各 1 单位代币;
当代币销毁时,相应释放出 1 USD;
整个系统的 USD 储备量始终与任意选项代币的供应量保持同步。
这套结构确保了:清算发生时,胜出的选项代币可以以 1 USD 的价格顺利赎回,从而满足第 2 条约束。
从价值守恒推导:为何价格自然归一
接下来我们看第 1 条:所有选项价格之和应为 1。
虽然看上去这是一个“价格结构”问题,但其实它可以从市场价值守恒原理推导而来:
系统的总价值 = 储备 USD 价值 = 所有预测资产的价值总和
数学表达如下:
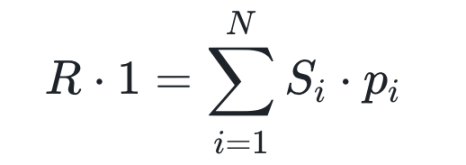
其中:
R:系统中的 USD 储备;
Si:第 i 个选项的代币供应量;
pi:第 i 个选项的市场价格。
根据前面的结论,系统设计要求 S_i=R ,代入得:
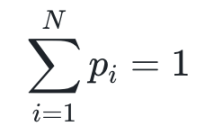
换句话说:只要资产和储备严格对等,价格归一将自然成立。
这使得价格总和为 1 成为系统内在结构的自然结果,而非需要强制校准。
相比之下,在 CLOB 模型中,价格由限价单撮合生成,且每个选项作为独立市场运作,若市场缺乏流动性或套利者,价格之间很难自然协调一致,因此经常出现概率之和 ≠ 1的情况,尤其在冷门预测市场中更为常见。
初始价格应灵活可控,避免系统性套利
初始价格设置在实践中尤为关键。若所有选项强制以对称价格(如 0.5/0.5)启动,则在明显倾斜的事件中将带来套利空间。
例如:
某一事件真实概率接近 99%,但初始价格设为 0.5;
用户可低价买入该选项,在价格回调前实现无风险套利;
造成损失的将是系统流动性提供者或早期交易者。
因此,一个优秀的协议机制必须支持事件发布者或系统根据上下文设定初始状态,包括:
允许注入非对称初始流动性;
设定目标价格点(如 YES = 0.9, NO = 0.1);
同时保持代币 - 储备结构不变,确保系统可逆性。
这正是 APMM 的优势所在,其机制允许灵活配置初始权重,防止激励失衡,同时保证数学约束不被破坏。
6.2 APMM 的交易过程
6.2.1 买入过程
用户存入 USD 并生成代币:
用户首先将 USDC 存入 APMM 流动性池,系统会根据存入的 USD 金额,等量生成每个选项的代币,例如,若有 3 个选项(A、B、C),系统会铸造相应数量的 A、B、C 代币。
选择目标选项代币:
用户根据自己的选择,将不想下注的选项代币在 APMM 内进行转换。例如,如果用户选择了 A 选项,系统会自动将其余的 B 和 C 选项代币转换为 A 选项代币。
完成交易:
最终,用户会收到完全由 A 选项代币组成的代币包,并且这笔交易会记录在 APMM 中,系统保留 USD 作为抵押品。
6.2.2 卖出过程
用户提交代币进行赎回:
用户希望卖出时,会将自己持有的某一选项代币(例如 A 选项)或多种选项代币打入 APMM 流动池中。
系统返回等量代币:
在卖出过程中,APMM 系统会根据用户提交的代币数量返回完全等量的所有选项代币(例如 A、B、C 代币)。
销毁代币并赎回 USD:
用户将收到的代币包销毁,然后从系统中赎回等值的 USD,完成卖出交易。此时,原始代币的价值变现为用户的 USD。
6.3 流动性池的设计
在前面的介绍中,我们已经理解了 APMM 的整体交易流程。而其中最核心的一环,正是代币在流动性池中的定价与兑换机制。
这一节我们将详细展开 APMM 中流动性池的数学结构。
流动性池的基本约束
在 APMM 的设计中,所有预测市场选项的代币都共存在一个统一的流动性池中,该池遵循如下的乘积不变公式:
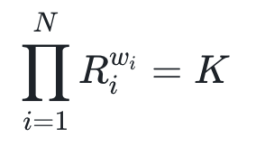
且
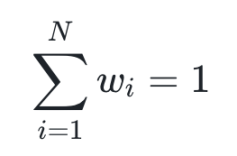
其中:
Ri:第 i 个选项代币在池中的储备(reserve)数量;
wi:该选项的权重系数
K:常数,用于维持池子的乘积不变性。
这个约束类似于常见 AMM 中的恒定乘积公式(如 Uniswap 的 x⋅y=k),但扩展到了多资产且加权版本。
买入过程
假设用户希望使用 a 单位 USD 买入某个预测市场的选项 1:
首先,用户按照标准铸造逻辑获得了总量为 a 的所有选项代币(每种各 a 单位);
然后,用户将非选中的所有代币(选项 2 至 N)注入流动性池;
系统将这些代币兑换为更多的选项 1 代币。
我们记兑换出的数量为 r1,则兑换后的新状态满足以下恒等式:
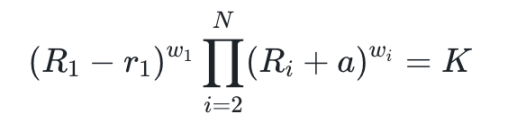
求解 r1 后,再加上最初铸造的 aaa 单位选项 1 代币,便得到用户最终获得的该选项代币总量 r1+a。
卖出过程
假设用户希望卖出 r1 单位的选项 1 代币,并换回 USD,我们记用户可以获得的 USD 数量为 u,则兑换后的系统状态应满足:
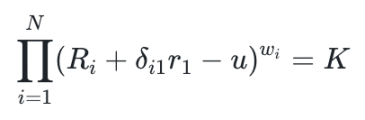
在这里计算出 u 的数量就可以知道用户能卖出多少 USD 了,不过这个计算是一个比较复杂的过程,我们通常需要牛顿速降法来计算。
APMM 同样支持同时卖出多种选项代币,这在用户希望一次性退出持仓、或“清仓”多个市场选项时尤其实用。
设 ri 为用户卖出的第 i 个选项代币数量,系统需满足:
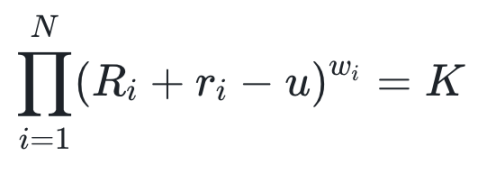
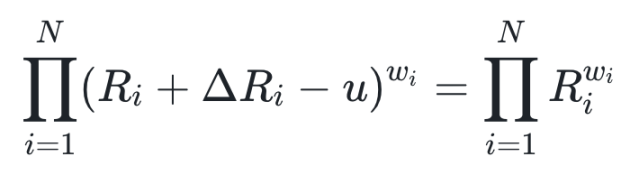
依旧是解出 u 得到用户可赎回的 USD 数量。
如何计算代币的价格?
你可能会注意到,APMM 的流动性池中并不直接存放 USD,这与 Uniswap 等传统 AMM 存在本质区别。因此我们无法直接通过 “一边 USD、一边代币” 的方式推导价格。
那么在这种结构下,如何定义预测市场中每个选项代币的价格呢?
在 APMM 中,预测市场选项代币的价格计算定义如下:
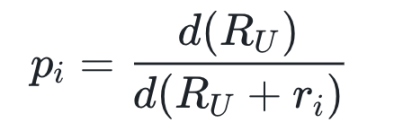
这是一微分表示形式,不过换一种方式就会更好理解,就是如果拿出微小的一些 USD(可能是 0.0....001USD),然后计算我能换出的预测市场代币的数量,然后除一除就可以了。
后面的计算可能需要一些数学背景,我这边就不在这里展开了。
直接给大家结论:
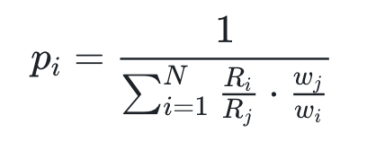
其中 pi 表示第 i 个选项代币的当前市场价格。
这个公式意味着,只要我们知道:
当前流动性池中所有选项代币的储备量 Ri;
每个选项的权重 wi;
就可以计算出任意一个选项代币的实时价格。
6.4 流动性池的初始化
在 APMM 中,预测市场的交易开始前,需要为每个市场配置初始流动性和初始价格。这一过程不仅决定了市场启动时的交易深度,也直接影响各选项的初始概率权重。
6.4.1 初始流动性的注入
当一个预测市场问题及其所有可能选项被确定之后,系统支持为其注入一笔初始流动性,以便立即开放交易。初始化过程如下:
设定总流动性规模:
例如,为某个预测市场设置初始流动性为 1000 USD。
铸造代币:
系统将这笔 1000 USD 质押进入储备池,并据此铸造出每个选项各 1000 单位的代币。
假设该市场有 N 个选项,则每个选项初始代币数量为 1000。
配置初始储备:
上述铸造的代币将作为 APMM 流动性池中各选项的初始 reserve(储备),即:
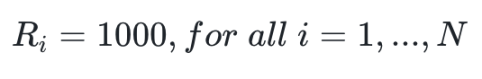
这样,预测市场就进入了“已初始化、可交易”的状态。
6.4.2 初始价格
APMM 中每个选项的价格,取决于当前的储备比例 Ri 和其对应的权重系数 wi。我们再次回顾上节的价格公式:
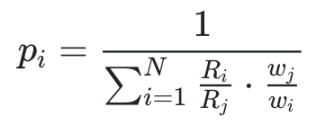
在市场初始化时,我们设定每个选项的储备相等,即:
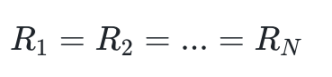
此时,公式可以简化为:
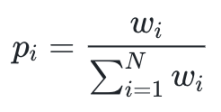
此外,由于
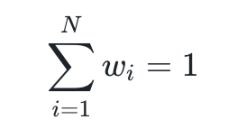
则
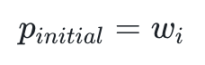
这意味着:每个选项的初始价格,等于其对应的权重系数 wi。因此当我们想要为不同选项设置初始价格的时候,只需要将 wi 设置成该选项的初始价格即可。
6.5 小结
本章尝试将 APMM 拆解为一个自洽的数学系统,并从交易流程、价格计算、流动性池构造、以及初始化机制四个角度逐层展开。
我们不仅展示了 APMM 是“可以跑起来”的,更揭示了它“为何能够成立”:每一个操作背后,都有清晰的守恒结构与推导基础作为支撑。
与其说 APMM 是一个做市工具,不如说它是一种机制语言:允许我们用确定性的公式,去组织不确定性的信念;用结构化的方式,引入自由开放的市场表达。
接下来的章节,我们将从「动机」转向「激励」,深入讨论 APMM 如何激活市场一侧最关键的参与者 —— 流动性提供者,以及如何将这套机制嫁接进一个真实产品之中。
07 流动性提供者的风险与激励
APMM 是一个高度依赖流动性的做市机制,流动性来自社区用户的主动贡献,而非中心化做市商。这一点与 Uniswap 的 AMM 十分类似。
但问题也随之而来:
如何激励用户持续为预测市场注入流动性?
又该如何平衡他们可能面临的风险?
在回答这个问题之前,我们先来明确流动性提供者在 APMM 中所处的风险结构。
7.1 无常损失:预测市场中的结构性风险
在传统 AMM 中,流动性提供者常面临“无常损失”(Impermanent Loss),即由于资产价格波动,导致其所持资产的价值低于单纯持有的收益。
而在预测市场中,这种损失的表现更加极端。
随着时间推移和信息不断揭示,市场价格往往逐渐向 0 或 1 收敛,这意味着最终流动性池中将残留大量“失败”选项的代币,其价值趋近于 0。
对于 LP 而言,这几乎是必然发生的亏损,而非“可能”的无常损失。
因此,仅靠传统手续费机制进行补偿,在预测市场中显得尤为不足。
7.2 动态手续费:为预测市场量身定制的补偿逻辑
在一般 AMM 中,为了激励 LP,系统会从交易中收取一定比例的手续费(如 1%),并将其分发给流动性提供者。
但在预测市场中,这种静态比例的费率存在明显问题:
如果某个选项价格已经接近 0.99,而手续费仍为 1%,那么用户买入后即使事件发生,其清算收益也无法覆盖成本,用户无论预测是否正确,都会亏钱——这显然是违背常理的。
为了解决这一问题,Bayes Labs 在 APMM 机制中引入了动态手续费机制(Dynamic Fee):
选项价格越接近 1,手续费越低;选项价格越接近 0,手续费越高。
这样设计带来了两个重要优势:
用户体验改善:即使在高概率选项中下注,用户仍然有正收益空间;
激励结构合理:手续费随交易风险而变化,保持对 LP 的补偿能力。
7.3 动态手续费的实现机制
动态手续费并不是直接从用户支付的 USD 中扣除,而是作用在用户交易过程中被用于兑换的代币部分。
以下是交易中的具体操作逻辑:
用户希望用 1 USD 购买选项 1 的代币,系统会先将 1 USD 对应的所有选项代币铸造出来(每种 1 单位),用户将非目标选项(即选项 2 到选项 N)的代币注入流动性池,系统将通过 APMM 为用户换出更多的选项 1 代币。
动态手续费不是从 1 USD 扣除,而是从注入池子的这些“非目标选项代币”中提取一部分。例如将选项 2 到选项 N 中各抽走 1%。
这样设计的妙处在于:
选项价格越高,代表兑换过程中需要用到的非目标代币价值越低,被收取的手续费自然就越低;
用户始终能从中获得“净增值”代币——即实际收到的目标选项代币总是多于 1 USD 等值;
无论市场处于什么阶段,用户都不会因手续费而陷入无意义的负收益区间。
7.4 手续费的去向与 LP 的真实收益
被收取的非目标代币(即手续费部分)最终将如何流转?
APMM 的处理方式也极具工程巧思:
系统会自动将这些代币兑换为 USD,并直接给予流动性的提供者;
LP 获得的是已经变现后的 USD 收益,而非一堆日后还需清算的“废币”;
7.5 小结
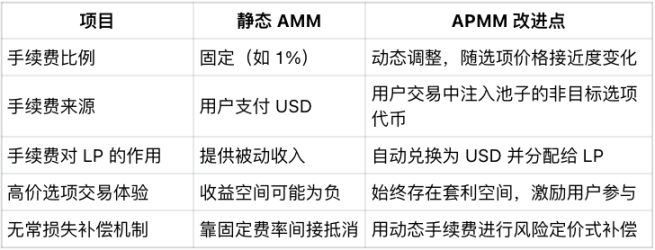
APMM 并没有回避预测市场中的结构性问题,而是正视它、对冲它、并借此创造更合理的流动性激励结构。
本章小结
本章围绕 APMM 的核心结构展开,重点介绍了其运行机制与流动性提供者的激励方式。
我们从交易流程入手,逐步推导价格模型、池子构造逻辑,并深入分析了如何通过动态手续费机制有效对冲无常损失,构建出更稳健、参与感更强的流动性系统。
虽然本章涉及较多数学内容,可能需要读者花一些时间细细消化,但相信这些基础将帮助你更深刻地理解 APMM 的创新所在。
在下一章节,我们将聚焦于 APMM 的流动性管理策略与真实场景下的应用实践。敬请期待,咱们不见不散!
往 期 回 顾

本次内容如果对你有所帮助,或者你对预测市场有兴趣。欢迎扫描下方二维码,加入我们的【预测市场社群】,我们将持续分享更多实用干货与答疑互动!
社群助理微信号
capybara2066
MT-GANDA
投稿、广告合作及授权
欢迎给公众号留言


【免责声明】市场有风险,投资需谨慎。本文不构成投资建议,用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资,责任自负。


